Engineering economic analysis: Difference between revisions
Tahirkapoor (talk | contribs) |
|||
| (48 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
Authors: Michael Gleeson,<sup> [2014] </sup> Sean Kelton,<sup> [2014] </sup> Thomas Considine,<sup> [2014] </sup> and Tahir Kapoor<sup> [2015] </sup> | |||
Stewards: David Chen, Jian Gong, and Fengqi You | |||
Date Presented: Feb. 22, 2014 | |||
==Introduction== | ==Introduction== | ||
Once equipment and operating costs are estimated, preliminary cash flow estimations can be performed to determine if the process is economically viable. When evaluating the long term economic return of a business, it is important to consider taxes, depreciation and amortization, and the time value of money. Once all economic factors are estimated, a discounted cash flow analysis can be used to quantitatively determine the economic return of the process. | |||
==Measures of Economic Return== | |||
The following are "back of the envelope" type calculations for economic return of a project. These measures are quick and easy because they ignore some of the more complicated parts of evaluating a project including factors such as depreciation, time value of money and taxes. | |||
===Payback Time=== | |||
The payback time is defined as the period of time (in years) required to break even on the initial economic investment. It is given by the equation: | |||
<math>T = I/C</math> | |||
Where <math>T</math> is the payback time for the project, <math>I</math> is the total investment required for the project and <math>C</math> is the average annual cash flow generated by the project. This calculation is used to determine how quickly the project's fixed costs (i.e. land, machinery, etc.) can be recovered from the project. A small payback period is desirable for a new project. | |||
===Return on Investment=== | |||
The regular return on investment (ROI) involves complicated tax and depreciation calculations. However, the pre-tax ROI is much simpler. It is given by the equation: | |||
<math>ROI = C/I</math> | |||
Where ROI in this case is the pre-tax ROI, C is the pre-tax cash flow generated by the project and I is the total investment required fro the project. This calculation, as it sounds, is a measure of the percentage return on the initial investment required for a project (typically the fixed costs, explained above). A higher ROI is a more profitable project. | |||
==Project Cash Flows== | |||
Project cash flows, much like it sounds, are the annualized cash flows, or revenue, generated from a new project. The first year of a project's cash flow is typically negative because the money is spent on initial investment. At first there will be a small expenditure on research and design expenses from engineering. Once the design is finished and construction is set to begin the expenditures will rapidly increase. These expenses may include things such as initial cost of renting or purchasing space/land, equipment & materials, initial labor to build a plant, etc. All in all research, design, procurement and construction, all which must be done prior to start up, will typically take 2-4 years. At this point the project will have reached maximum investment and typically has the most negative sum of cash flows. | |||
The first year after start up, cash flows begin to become positive, however, the cash flows in the first year are usually reduced comparatively to years after. This is due to unexpected problems within the project/process. Typically machine down time, maintenance,etc. will be greatest in this year, causing the project to run under capacity. After the first year all of the problems within a process have begun to be discovered and resolved and so the process can run at full capacity with increase cash flows. From this point on, the only improvements in project cash flows come from process improvements (i.e. six sigma analysis, etc.), however, by using these techniques project cash flows can become greater year over year. | |||
Toward the end of the life of a project, cash flows can begin to tail off in magnitude once again due to outdated equipment, new competition, or other increases in operating costs. Finally when a project is terminated there is a small additional cash flow related to the recovery from any assets such as equipment, land, etc. can all be resold or scrapped, however, there will also be some amount of costs related to deconstruction and land remediation (due to pollution or other harmful project outputs). Typically the recovered assets outweighs these costs. | |||
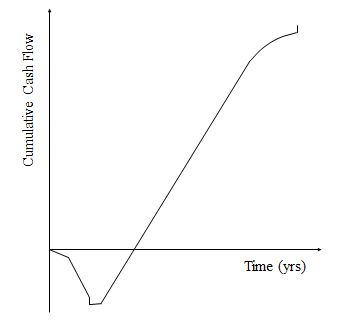
A typical cash flow diagram of a project relating the cumulative cash flows over the life of the project is shown in the figure below. | |||
[[File:Example11.jpg]] | |||
Figure 1: Cash Flows Diagram. Taken from ChE 351 powerpoint slide 11 (written by Jennifer Cole) for class instruction. Slides presented on Oct. 5, 2013. | |||
As seen in Figure 1, the cash flows follow the pattern described in the paragraph above. The break even point of the project is the point at which the cash flows cross the x-axis. The life of the project is given by the duration of the graph. | |||
==Taxes== | ==Taxes== | ||
| Line 6: | Line 45: | ||
===Corporate Taxes=== | ===Corporate Taxes=== | ||
While tax codes can vary from state to state, and from county to county. Looking at the federal tax rate is one measure of the tax rate. Federal tax rates for different income are detailed in the table below. It is important to note that taxes are levied on income only and not on revenue. | |||
{| class="wikitable" style="margin: 1em auto 1em auto;" | |||
! '''Taxable Income ($)''' || '''Tax Rate''' <sup> [1] </sup> | |||
|- | |||
| 0 to 50,000 || 15% | |||
|- | |||
| 50,000 to 75,000 || $7,500 + 25% Of the amount over 50,000 | |||
|- | |||
| 75,000 to 100,000 || $13,750 + 34% Of the amount over 75,000 | |||
|- | |||
| 100,000 to 335,000 || $22,250 + 39% Of the amount over 100,000 | |||
|- | |||
| 335,000 to 10,000,000 || $113,900 + 34% Of the amount over 335,000 | |||
|- | |||
| 10,000,000 to 15,000,000 || $3,400,000 + 35% Of the amount over 10,000,000 | |||
|- | |||
| 15,000,000 to 18,333,333 || $5,150,000 + 38% Of the amount over 15,000,000 | |||
|- | |||
| 18,333,333 and up || 35% | |||
|} | |||
Many companies have much lower effective tax rates due to tax breaks and loopholes. When deducting taxes, simply assuming a corporate tax rate of 35% can greatly overestimate the amount of taxes that a company pays. A better estimation of tax rates would be to find the effective tax rate of similar publicly traded corporations. The tax rate of any publicly traded company can be found on their quarterly reports (Form 10-Q) or their annual reports (Form 10-K) filed with the SEC. Below are some effective tax rates of major chemical companies for 2014 (2013 for The Dow Chemical Company). <sup> [2] </sup> | |||
{| class="wikitable" style="margin: 1em auto 1em auto;" | |||
|+ '''Tax Rate of Selected Chemical Companies''' | |||
! scope="col" | Company | |||
! scope="col" | WACC | |||
|- | |||
| The Dow Chemical Company || 29.2% | |||
|- | |||
| Exxon Mobil Corporation || 41% | |||
|- | |||
| Monsanto Company || 28% | |||
|} | |||
===Investment Incentives=== | ===Investment Incentives=== | ||
| Line 15: | Line 86: | ||
Local, state, and federal governments generally encourage capital investments by corporations. Financial incentives afforded to corporations include low interest loans, free capital for research and development, and tax holidays for new technologies. | Local, state, and federal governments generally encourage capital investments by corporations. Financial incentives afforded to corporations include low interest loans, free capital for research and development, and tax holidays for new technologies. | ||
Recently, large investment incentives have been provided for green energy technologies. The major federal program responsible for green investment incentive, comes in the form of a tax credit for green technologies. Valid until December 31, 2016 the following technologies can be used to claim tax incentives. | |||
{| class="wikitable" style="margin: 1em auto 1em auto;" | |||
|+ '''Incentives for Green Energy Technologies''' | |||
! Technology | |||
! Investment Incentive | |||
|- | |||
| Solar | |||
| 30% of expenditures | |||
|- | |||
| Fuel Cell | |||
| 30% of expenditures (up to $1500 per 0.5 kW) | |||
|- | |||
| Small Wind Turbines (Max 100 kW) | |||
| 30% of expenditure | |||
|- | |||
| Geothermal Systems | |||
| 10% of expenditure | |||
|- | |||
| Microturbines | |||
| 10% of expenditure (up to $200 per kW) | |||
|- | |||
| Combined Heat and Power | |||
| 10% of expenditure (up to 50 MW capacity and must be over 60% efficient) | |||
|} | |||
Many other investment incentives are available to companies making large investments, but they are extremely difficult to estimate and are often very specific depending on location and type of project. | |||
==Depreciation== | ==Depreciation== | ||
| Line 33: | Line 132: | ||
<math>D</math> is the depreciation; and | <math>D</math> is the depreciation; and | ||
<math>t</math> are the taxes due. | <math>t</math> are the taxes due. | ||
Two commons methods of calculating depreciation are discussed in the next sections. | |||
===Straight Line Depreciation=== | ===Straight Line Depreciation=== | ||
=== | Straight line depreciation is the most common method of approximating depreciation when calculating profitability measures, such as return on investment (Seider, 392). | ||
In this method, the depreciable value <math>Cd</math> is written off over the total life of <math>n</math> years at a constant linear rate: | |||
<math>Di=Cd/n</math>, where <math>i</math> is each year in the lifetime. | |||
Therefore, the book value <math>Bm</math>, or the initial cost of the item minus the accumulated depreciation charges, at year <math>m</math>, can be defined as: | |||
<math>Bm=C-m*Cd/n</math> where <math>C</math> is the initial cost of the item. | |||
===Depreciation Case Study=== | |||
For example, let us find the book value after 3 years of a compressor which originally costs $50,000, has a depreciable value of $5,000, and has a lifetime of 20 years. | |||
<math>Di=5,000/20=250</math> | |||
<math>Bm=$50,000-250*3=$49,250</math> | |||
Therefore we can say that over the three years, the compressor has cost the process a difference of $750, which can be taken out of the taxable income. | |||
==Time Value of Money== | |||
Money that is available now is inherently more valuable than the same amount in the future, because that money could be used as capital for an investment that earns interest. | |||
Capital that is available in the future is said to be "discounted". The present value of money, which is discussed in further detail in the coming sections, is a discounted amount of the future value: | |||
<math>PV=FV*DF</math>. | |||
Where <math>PV</math> is the Present value, <math>FV</math> is the Future value, and <math>DF</math> is the discount factor. | |||
The discount factor, which takes into account an estimated interest rate gained on present money, is calculated for every year <math>n</math>: | |||
<math>DF=1/(1+i)^n</math>. | |||
This implies that the a given amount of money in the future has less value as the length of future time increases, and as the expected amount of interest that current capital could gain increases. See Net Present Value for more information on this subject. | |||
Of additional interest is the different between the time value of money and inflation. It is important to note that these two concepts are completely different. Inflation is the yearly rate at which the price of a certain good will increase (Biegler, 169). Although the mathematics and calculations are similar, inflation is generally a result of socioeconomic factors increasing the supply of money, and not the potential interest rate gained on current capital. | |||
==Discounted Cash Flow Methods== | |||
As discussed above, the value of money is directly related to time, insofar as $500 today is worth more than $500 in two years. Discounted cash flow methods, such as net present value (NPV) and internal rate of return (IRR) take the time value of money into account. The main difference between nondiscounted and discounted cash flows is that all cash flows are related to time zero in the latter.(Turton 266). | |||
===Net Present Value=== | |||
Net Present Value (NPV), also known as Net Present Worth (NPW), gives the present value of all payments and provides a basis of comparison for projects with different payment schedules but similar lifetimes. (Biegler 151). In making comparisons between projects, the larger the net present worth, the more favorable the investment. (Peters 328). It is one of the most widely used economic measures because it captures the time value of money, the value of investment incentives and variations in construction schedule, while allowing for price forecast models that include cyclic behavior. The NPV can be represented as: | |||
<math> NPV = \sum_{n=1}^{n=t}\frac{CF_n} {\left( 1+i \right) ^n} </math> | |||
where <math>CF_n</math> = cash flow in year n and <math>t</math> = project lifetime and i is the discount rate as a decimal. (Towler 407). If the net present value is equal to zero, the return of the project is equal to the return that the discount rate would provide. (Peters 328). There are several drawbacks to NPV; it does not measure bang for buck, and it cannot be optimized unless an upper bound is set to the plant size. | |||
===Discounted Cash Flow Rate of Return=== | |||
The DCFROR is the interest or discount rate for which the NPV is equal to zero. (Turton 270). This means that DCFROR represents the highest after tax interest rate at which the project can break even. Often, corporation management will set an "internal" interest rate, which is the lowest rate of return that a company will accept for any new investment. If the DCFROR is greater than this internal rate, the investment is favorable. NPV and DCFROR are almost always used together. (Peters 328). The DCFROR can be represented as: | |||
<math>\sum_{n=1}^{n=t}\frac{CF_n} {\left( 1+i' \right) ^n} = 0 </math> | |||
where i' is the DCFROR. DCFROR is useful for comparing projects of different sizes and for comparing projects to other investments. (Towler 408). | |||
===Discounted Payback Period=== | |||
DPP is the time required, after start-up, to recover the fixed capital costs required for a project with all cash flows discount back to time zero. (Turton 268). The project with the shortest discounted payback period is the most desirable. | |||
===Example – Calculating NPV=== | |||
Using the following projected cash flow statement, calculate the net present value using the 10 year AA corporate bond rate of 2.78%. | |||
{| class="wikitable" style="margin: 1em auto 1em auto;" | |||
! Year: | |||
! 1 | |||
! 2 | |||
! 3 | |||
! 4 | |||
! 5 | |||
! 6 | |||
! 7 | |||
! 8 | |||
! 9 | |||
! 10 | |||
! 11 | |||
! 12 | |||
|- | |||
| Revenue | |||
| $ - | |||
| $ - | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
|- | |||
| Capital Expenditures | |||
| $ (45.00) | |||
| $ (40.00) | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
|- | |||
| Operating Costs | |||
| $ - | |||
| $ - | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
|- | |||
| Depreciation | |||
| $ - | |||
| $ - | |||
| $ (17.00) | |||
| $ (27.20) | |||
| $ (16.32) | |||
| $ (9.79) | |||
| $ (9.79) | |||
| $ (4.90) | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
|- | |||
| Taxes | |||
| $ - | |||
| $ - | |||
| $ (2.61) | |||
| $ 0.35 | |||
| $ (2.81) | |||
| $ (4.70) | |||
| $ (4.70) | |||
| $ (6.12) | |||
| $ (7.54) | |||
| $ (7.54) | |||
| $ (7.54) | |||
| $ (7.54) | |||
|- | |||
| Free Cash Flow | |||
| $ (45.00) | |||
| $ (40.00) | |||
| $ 23.39 | |||
| $ 26.35 | |||
| $ 23.19 | |||
| $ 21.30 | |||
| $ 21.30 | |||
| $ 19.88 | |||
| $ 18.46 | |||
| $ 18.46 | |||
| $ 18.46 | |||
| $ 18.46 | |||
|} | |||
<math> NPV = \sum_{n=1}^{n=t}\frac{CF_n} {\left( 1+i \right) ^n} </math> | |||
<math> NPV = \frac{-45} {\left( 1+0.0278 \right) ^1} + \frac{-40} {\left( 1+0.0278 \right) ^2}+ \frac{23.39} {\left( 1+0.0278 \right) ^3}+ \frac{26.35} {\left( 1+0.0278 \right) ^4} + \text{. . . .} + \frac{18.46} {\left( 1+0.0278 \right) ^{11}}+ \frac{18.46} {\left( 1+0.0278 \right) ^{12}} </math> | |||
<math> NPV = 90.73 </math> | |||
A Net Present Value of 90.73 was obtained. | |||
==Annualized Costs== | |||
Annualized Cost is another way of comparing capital expenses with future cash flows where the capital expense is converted into a recurring annual capital charge. It is useful for comparing the cost of assets with different lifetimes. (Towler 411). This is very similar to the way that mortgages are amortized over a 15 or 30 year lifetime. Annual payment can be represented as: | |||
<math>A = P\,\frac{i\,\left( 1+i \right)^n} {\left(1+i\right)^n - 1}</math> | |||
where P is the principle investment, n is investment period, and i is the discount rate. The annual capital charge ratio can be defined as: | |||
<math>ACCR = A/P</math> | |||
It is the fraction of the principle that must be paid each year to recover the investment at the target interest rate. | |||
== Estimating the Discount Rate == | |||
Small changes in the discount rate, can cause large fluctuations in future cash flow. When projecting project cash flows many years in the future it is essential that an accurate discount rate is chosen to get a reasonable cost estimation. A simple estimation of the discount rate is to set it equal to the interest rate received from bonds. | |||
<math> D = i </math> | |||
This simple estimation will often yield a result greatly under a value needed for a good cost estimations because in the modern financial economy, cash deposits yield minimal interest rates. Many other forms of higher yielding securities are available to investors and a good discount rate should combine the interest from many different sources rather than just cash deposits. | |||
===Weighted- Average Cost of Capital. (WACC) === | |||
The weighted average cost of capital is a rate that a company is expected to pay to all of its shareholders to finance all of its assets and liabilities (debt, equity, etc.). The WACC is not a rate set by management, but is rather an implied rate that the company must return to shareholders or else they will start selling shares to invest elsewhere and depress the company’s value. Due to this reason, WACC rates for the same company can be evaluated to different estimations depending on calculation method. | |||
Generally, WACC is described by the following formula: <sup> [3] </sup> | |||
<math>\text{WACC} = \frac{\sum_{i=1}^N r_i \cdot MV_i }{\sum_{i=1}^N MV_i}</math> | |||
where <math>N</math> is the number of sources of capital (securities, types of liabilities); <math>r_i</math> is the required rate of return for security <math>i</math>; and <math>MV_i</math> is the market value of all outstanding securities <math>i</math>. | |||
The WACC is often simplified to include only debt and equity. Thus it can be written as | |||
<math>\text{WACC} = \frac{E}{E+D}r_e + \frac{D}{E+D}r_d</math> | |||
where <math> E</math> is the total market value of shareholder’s equity, <math> D</math> is the total market value of debt, <math> r_e</math> is the cost of equity, and <math> r_d</math> is the cost of debt. <sup> [4] </sup> | |||
====Cost of Equity==== | |||
The cost of equity is analogous to the returns that shareholders expect in return from giving a company their equity through share purchases. | |||
<math> r_e = r_f + (\beta)RP</math> | |||
where <math> r_f</math> is the risk free rate of return that investors in stable securities such as US treasury bonds can expect. <math> \beta</math> is a commonly used factor describing the company’s stock’s correlation with the general market. <math> RP</math> is the risk premium, the rate of return that investors expect by investing in a stock rather than a more stable class of security. A risky company will have a higher risk premium. <sup> [5] </sup> | |||
====Cost of Debt==== | |||
The cost of debt, <math> r_d</math>, is either a fixed or variable rate that a company pays to a lender. This rate has been renegotiated and can be easily looked up. Since debt is tax deductible, taxes are often discounted. | |||
====WACC equation==== | |||
<math>\text{WACC} = \frac{E}{E+D}( r_f + (\beta)RP) + \frac{D}{E+D}(r_d(1-T))</math> | |||
Where <math> \ T</math> is the tax rate. | |||
Many of the inputs required to calculate WACC can be easily obtained from a publicly traded company’s financial statements. An example of some WACCs of major chemical companies as of 2/6/15 are shown in the following table. <sup> [6] </sup> | |||
{| class="wikitable" style="margin: 1em auto 1em auto;" | |||
|+ '''WACC of Selected Chemical Companies''' | |||
! scope="col" | Company | |||
! scope="col" | WACC | |||
|- | |||
| The Dow Chemical Company || 7.01% | |||
|- | |||
| Exxon Mobil Corporation || 11.64% | |||
|- | |||
| Monsanto Company || 9.23% | |||
|} | |||
===Example – Comparing Interest Rate and WACC methods=== | |||
Using the same projected cash flow statement as in the example of calculating NPV above, calculate the net present value using the WACC of Dow chemical company and compare it to the 10 year AA corporate bond rate. | |||
{| class="wikitable" style="margin: 1em auto 1em auto;" | |||
! Year: | |||
! 1 | |||
! 2 | |||
! 3 | |||
! 4 | |||
! 5 | |||
! 6 | |||
! 7 | |||
! 8 | |||
! 9 | |||
! 10 | |||
! 11 | |||
! 12 | |||
|- | |||
| Revenue | |||
| $ - | |||
| $ - | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
| $ 38.00 | |||
|- | |||
| Capital Expenditures | |||
| $ (45.00) | |||
| $ (40.00) | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
|- | |||
| Operating Costs | |||
| $ - | |||
| $ - | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
| $ (12.00) | |||
|- | |||
| Depreciation | |||
| $ - | |||
| $ - | |||
| $ (17.00) | |||
| $ (27.20) | |||
| $ (16.32) | |||
| $ (9.79) | |||
| $ (9.79) | |||
| $ (4.90) | |||
| $ - | |||
| $ - | |||
| $ - | |||
| $ - | |||
|- | |||
| Taxes | |||
| $ - | |||
| $ - | |||
| $ (2.61) | |||
| $ 0.35 | |||
| $ (2.81) | |||
| $ (4.70) | |||
| $ (4.70) | |||
| $ (6.12) | |||
| $ (7.54) | |||
| $ (7.54) | |||
| $ (7.54) | |||
| $ (7.54) | |||
|- | |||
| Free Cash Flow | |||
| $ (45.00) | |||
| $ (40.00) | |||
| $ 23.39 | |||
| $ 26.35 | |||
| $ 23.19 | |||
| $ 21.30 | |||
| $ 21.30 | |||
| $ 19.88 | |||
| $ 18.46 | |||
| $ 18.46 | |||
| $ 18.46 | |||
| $ 18.46 | |||
|} | |||
To calculate Dow Chemical’s WACC, we need the following information | |||
* Total Equity, <math>E</math> | |||
* Total Debt, <math>D</math> | |||
* Corporate Tax Rate, <math>T</math> | |||
* Cost of Debt, <math>r_d</math> | |||
* Cost of Equity, <math>r_e</math> | |||
Unlike total equity, total debt and the corporate tax rate, the cost of debt and the cost of equity are not concrete numbers that are reported by most publicly traded companies. The cost of debt can be calculated by using the amount of interest that a company pays on their total debt while the cost of equity can be calculated by estimating the risk free rate, the risk premium for a market and the beta of the company. The risk free rate and the risk premium can vary slightly from model to model, but the beta is easily obtained from any financial website. | |||
To calculate the cost of debt and the cost of equity we need the following information. | |||
* Cost of Debt, <math>r_d</math> | |||
** Total Debt, <math>D</math> | |||
** Interest Payments, <math>I</math> | |||
* Cost of Equity, <math>r_e</math> | |||
** Risk Free Rate, <math>r_e</math> | |||
** Beta, <math> \beta</math> | |||
** Risk Premium, <math>RP</math> | |||
Many of these variables can be easily obtained by examining Dow Chemical’s corporate filings. To find, <math>E</math>, <math>D</math>, <math>I</math>, and <math>T</math>, we can look at Dow’s annual report for 2014 found via the SEC. (http://www.sec.gov/Archives/edgar/data/29915/000002991515000011/dow201410k.htm) | |||
{| class="wikitable" style="margin: 1em auto 1em auto;" | |||
| Total Equity | |||
|$ 22,423,000,000.00 | |||
|- | |||
| Total Debt | |||
| $ 18,838,000,000.00 | |||
|- | |||
| Interest Payments | |||
| $ 1,002,000,000.00 | |||
|- | |||
| Tax Rate | |||
| 27.1% | |||
|} | |||
Using these figures, the cost of debt can be calculated: | |||
<math> r_d = I/D = (1002000000/18838000000)= 5.32%</math> | |||
To calculate the cost of equity, the risk free rate and the risk premium need to be estimated. US treasury bonds are typically used as the benchmark for a risk free investment and the yield for a 10 year treasury bond was taken to be the risk free rate. The risk premium was taken to be the average return of the S&P 500 stock index over the previous 10 years. Finally the beta was obtained from Yahoo Finance. | |||
{| class="wikitable" style="margin: 1em auto 1em auto;" | |||
| Beta | |||
| 0.75 | |||
|- | |||
| Risk Free Rate | |||
| 2.24% | |||
|- | |||
| Risk Premium | |||
| 9.37% | |||
|} | |||
Using these values, the cost of equity can be calculated: | |||
<math> r_e = r_f + \beta*RP = 2.24 +0.75*9.37 = 9.27%</math> | |||
With all necessary parameters obtained, we can estimate Dow Chemical’s WACC: | |||
<math>\text{WACC} = \frac{E}{E+D}( r_e) + \frac{D}{E+D}(r_d(1-T))</math> | |||
<math>\text{WACC} = \frac{22423}{22423+18838}( 0.0927) + \frac{18838}{22423+18838}(0.0532(1-0.271))</math> | |||
<math>\text{WACC} = 6.81% </math> | |||
After WACC is obtained, we can compare the NPV using the WACC as the discount rate vs using the 10 year AA corporate bond rate as the discount rate. | |||
The NPV using the 10 year AA corporate bond rate of 2.78% was found to be 90.73 in the previous example. | |||
Calculate the NPV using a WACC of 6.81% | |||
<math> NPV = \frac{-45} {\left( 1+0.0681 \right) ^1} + \frac{-40} {\left( 1+0.0681 \right) ^2}+ \frac{23.39} {\left( 1+0.0681 \right) ^3}+ \frac{26.35} {\left( 1+0.0681 \right) ^4} + \text{. . . .} + \frac{18.46} {\left( 1+0.0681 \right) ^{11}}+ \frac{18.46} {\left( 1+0.0681 \right) ^{12}} </math> | |||
<math> NPV = 55.51 </math> | |||
{| class="wikitable" style="margin: 1em auto 1em auto;" | |||
|+ '''Comparing NPV using Interest Rates and WACC''' | |||
| WACC | |||
| 55.51 | |||
|- | |||
| 10 Year AA Corporate Bond Rate | |||
| 90.73 | |||
|} | |||
Using the 10 year AA corporate bond yield as an interest rate results in a substantial difference in net present value than using Dow Chemical’s WACC. This example highlights the need to accurately estimate the discount rate to achieve a reasonable economic evaluation. | |||
==Conclusion== | |||
Measures of economic return are vital in the design phase of an engineering project. Companies will perform simulations to project capital and operating cost expenditures along with revenue generation, and use the resulting data to perform economic analyses, such as NPV, payback period, or discounted cash flow analysis. Based on the results of this analysis, the project will either be scrapped or it will be given the go ahead to begin granular design and construction. These measures of economic return can be very sensitive to the tax rate, discount rate, and other financial factors and it is very important to provide reasonable values of these parameters to get an accurate economic return. Measures of economic return provide a quick way for companies to determine the feasibility of a project, and therefore are extremely valuable. | |||
==References== | |||
= | # Biegler L, Grossmann I, Westerberg A, ''Systematic Methods of Chemical Process Design'', Prentice-Hall: Upper Saddle River, 1997. | ||
#Douglas J, Conceptual Design of Chemical Processes, McGraw-Hill: New York, 1988. | |||
# "EDGAR Search Results." EDGAR Search Results. U.S. Securities and Exchange Commission, n.d. Web. 06 Feb. 2015. | |||
# Fernandes N. 2014, Finance for Executives: A Practical Guide for Managers, p. 32. | |||
#"DCF Analysis: Calculating The Discount Rate | Investopedia." Investopedia. Investopedia, 03 Jan. 2006. Web. 06 Feb. 2015. | |||
#Form 1120 Instructions for 2012 page 17 | |||
# Frank, Murray; Shen, Tao (2012). "Investment, Q, and the Weighted Average Cost of Capital".http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2014367. | |||
# Miles J, Ezzell J. (September 1980). "The weighted average cost of capital, perfect capital markets and project life: a clarification". Journal of Financial and Quantitative Analysis 15 (3): 719–730.doi:10.2307/2330405. | |||
# Peters M, Timmerhaus K, "Plant Design and Economics for Chemical Engineers", 5th Ed., McGraw-Hill: New York, 2003 | |||
# Sieder W, Seader J, Lewin D, ''Process Design Principles: Synthesis, Analysis, and Evaluation'', Wiley: New York, 2004. | |||
# Towler G, Sinnott R, ''Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design'', Elsevier, 2012. | |||
# Turton R, Bailie R, Whiting W, Shaeiwitz J, ''Analysis, Synthesis, and Design of Chemical Processes'', Prentice Hall: Upper Saddle River, 2003. | |||
Latest revision as of 22:57, 8 March 2015
Authors: Michael Gleeson, [2014] Sean Kelton, [2014] Thomas Considine, [2014] and Tahir Kapoor [2015]
Stewards: David Chen, Jian Gong, and Fengqi You
Date Presented: Feb. 22, 2014
Introduction
Once equipment and operating costs are estimated, preliminary cash flow estimations can be performed to determine if the process is economically viable. When evaluating the long term economic return of a business, it is important to consider taxes, depreciation and amortization, and the time value of money. Once all economic factors are estimated, a discounted cash flow analysis can be used to quantitatively determine the economic return of the process.
Measures of Economic Return
The following are "back of the envelope" type calculations for economic return of a project. These measures are quick and easy because they ignore some of the more complicated parts of evaluating a project including factors such as depreciation, time value of money and taxes.
Payback Time
The payback time is defined as the period of time (in years) required to break even on the initial economic investment. It is given by the equation:
Where is the payback time for the project, is the total investment required for the project and is the average annual cash flow generated by the project. This calculation is used to determine how quickly the project's fixed costs (i.e. land, machinery, etc.) can be recovered from the project. A small payback period is desirable for a new project.
Return on Investment
The regular return on investment (ROI) involves complicated tax and depreciation calculations. However, the pre-tax ROI is much simpler. It is given by the equation:
Where ROI in this case is the pre-tax ROI, C is the pre-tax cash flow generated by the project and I is the total investment required fro the project. This calculation, as it sounds, is a measure of the percentage return on the initial investment required for a project (typically the fixed costs, explained above). A higher ROI is a more profitable project.
Project Cash Flows
Project cash flows, much like it sounds, are the annualized cash flows, or revenue, generated from a new project. The first year of a project's cash flow is typically negative because the money is spent on initial investment. At first there will be a small expenditure on research and design expenses from engineering. Once the design is finished and construction is set to begin the expenditures will rapidly increase. These expenses may include things such as initial cost of renting or purchasing space/land, equipment & materials, initial labor to build a plant, etc. All in all research, design, procurement and construction, all which must be done prior to start up, will typically take 2-4 years. At this point the project will have reached maximum investment and typically has the most negative sum of cash flows.
The first year after start up, cash flows begin to become positive, however, the cash flows in the first year are usually reduced comparatively to years after. This is due to unexpected problems within the project/process. Typically machine down time, maintenance,etc. will be greatest in this year, causing the project to run under capacity. After the first year all of the problems within a process have begun to be discovered and resolved and so the process can run at full capacity with increase cash flows. From this point on, the only improvements in project cash flows come from process improvements (i.e. six sigma analysis, etc.), however, by using these techniques project cash flows can become greater year over year.
Toward the end of the life of a project, cash flows can begin to tail off in magnitude once again due to outdated equipment, new competition, or other increases in operating costs. Finally when a project is terminated there is a small additional cash flow related to the recovery from any assets such as equipment, land, etc. can all be resold or scrapped, however, there will also be some amount of costs related to deconstruction and land remediation (due to pollution or other harmful project outputs). Typically the recovered assets outweighs these costs.
A typical cash flow diagram of a project relating the cumulative cash flows over the life of the project is shown in the figure below.
Figure 1: Cash Flows Diagram. Taken from ChE 351 powerpoint slide 11 (written by Jennifer Cole) for class instruction. Slides presented on Oct. 5, 2013.
As seen in Figure 1, the cash flows follow the pattern described in the paragraph above. The break even point of the project is the point at which the cash flows cross the x-axis. The life of the project is given by the duration of the graph.
Taxes
Chemical production facilities are subject to the same financial levies by the government as all corporations. Specifically, corporations typically pay income taxes, and may collect incentives based on state and federal regulations. Detailed tax filings are almost always conducted by the accounting or financial department of a corporation. When preparing process economics estimations, taxes should be included, however all final cost estimates reported to management should be prepared by the appropriate specialist (Douglas, 23).
Corporate Taxes
While tax codes can vary from state to state, and from county to county. Looking at the federal tax rate is one measure of the tax rate. Federal tax rates for different income are detailed in the table below. It is important to note that taxes are levied on income only and not on revenue.
| Taxable Income ($) | Tax Rate [1] |
|---|---|
| 0 to 50,000 | 15% |
| 50,000 to 75,000 | $7,500 + 25% Of the amount over 50,000 |
| 75,000 to 100,000 | $13,750 + 34% Of the amount over 75,000 |
| 100,000 to 335,000 | $22,250 + 39% Of the amount over 100,000 |
| 335,000 to 10,000,000 | $113,900 + 34% Of the amount over 335,000 |
| 10,000,000 to 15,000,000 | $3,400,000 + 35% Of the amount over 10,000,000 |
| 15,000,000 to 18,333,333 | $5,150,000 + 38% Of the amount over 15,000,000 |
| 18,333,333 and up | 35% |
Many companies have much lower effective tax rates due to tax breaks and loopholes. When deducting taxes, simply assuming a corporate tax rate of 35% can greatly overestimate the amount of taxes that a company pays. A better estimation of tax rates would be to find the effective tax rate of similar publicly traded corporations. The tax rate of any publicly traded company can be found on their quarterly reports (Form 10-Q) or their annual reports (Form 10-K) filed with the SEC. Below are some effective tax rates of major chemical companies for 2014 (2013 for The Dow Chemical Company). [2]
| Company | WACC |
|---|---|
| The Dow Chemical Company | 29.2% |
| Exxon Mobil Corporation | 41% |
| Monsanto Company | 28% |
Investment Incentives
Local, state, and federal governments generally encourage capital investments by corporations. Financial incentives afforded to corporations include low interest loans, free capital for research and development, and tax holidays for new technologies.
Recently, large investment incentives have been provided for green energy technologies. The major federal program responsible for green investment incentive, comes in the form of a tax credit for green technologies. Valid until December 31, 2016 the following technologies can be used to claim tax incentives.
| Technology | Investment Incentive |
|---|---|
| Solar | 30% of expenditures |
| Fuel Cell | 30% of expenditures (up to $1500 per 0.5 kW) |
| Small Wind Turbines (Max 100 kW) | 30% of expenditure |
| Geothermal Systems | 10% of expenditure |
| Microturbines | 10% of expenditure (up to $200 per kW) |
| Combined Heat and Power | 10% of expenditure (up to 50 MW capacity and must be over 60% efficient) |
Many other investment incentives are available to companies making large investments, but they are extremely difficult to estimate and are often very specific depending on location and type of project.
Depreciation
Depreciation, in the colloquial sense, is the loss of value of an item. As it pertains to the chemical process industry, depreciation is the loss of value due to "wear and tear" of the components and facilities of the plant. It is important to note that this does not include working capital or land.
Economics of Depreciation
Depreciation can be thought of as a yearly expense that the plant incurs. It can then be considered a cost, effectively reducing the income and thus the income tax. However, depreciation is not an actual cash flow. There is no transfer of money.
Note how depreciation lowers the amount of taxes:
where is the taxes due; is the gross profit; is the depreciation; and are the taxes due.
Two commons methods of calculating depreciation are discussed in the next sections.
Straight Line Depreciation
Straight line depreciation is the most common method of approximating depreciation when calculating profitability measures, such as return on investment (Seider, 392).
In this method, the depreciable value is written off over the total life of years at a constant linear rate:
, where is each year in the lifetime.
Therefore, the book value , or the initial cost of the item minus the accumulated depreciation charges, at year , can be defined as:
where is the initial cost of the item.
Depreciation Case Study
For example, let us find the book value after 3 years of a compressor which originally costs $50,000, has a depreciable value of $5,000, and has a lifetime of 20 years.
Therefore we can say that over the three years, the compressor has cost the process a difference of $750, which can be taken out of the taxable income.
Time Value of Money
Money that is available now is inherently more valuable than the same amount in the future, because that money could be used as capital for an investment that earns interest.
Capital that is available in the future is said to be "discounted". The present value of money, which is discussed in further detail in the coming sections, is a discounted amount of the future value:
.
Where is the Present value, is the Future value, and is the discount factor.
The discount factor, which takes into account an estimated interest rate gained on present money, is calculated for every year :
.
This implies that the a given amount of money in the future has less value as the length of future time increases, and as the expected amount of interest that current capital could gain increases. See Net Present Value for more information on this subject.
Of additional interest is the different between the time value of money and inflation. It is important to note that these two concepts are completely different. Inflation is the yearly rate at which the price of a certain good will increase (Biegler, 169). Although the mathematics and calculations are similar, inflation is generally a result of socioeconomic factors increasing the supply of money, and not the potential interest rate gained on current capital.
Discounted Cash Flow Methods
As discussed above, the value of money is directly related to time, insofar as $500 today is worth more than $500 in two years. Discounted cash flow methods, such as net present value (NPV) and internal rate of return (IRR) take the time value of money into account. The main difference between nondiscounted and discounted cash flows is that all cash flows are related to time zero in the latter.(Turton 266).
Net Present Value
Net Present Value (NPV), also known as Net Present Worth (NPW), gives the present value of all payments and provides a basis of comparison for projects with different payment schedules but similar lifetimes. (Biegler 151). In making comparisons between projects, the larger the net present worth, the more favorable the investment. (Peters 328). It is one of the most widely used economic measures because it captures the time value of money, the value of investment incentives and variations in construction schedule, while allowing for price forecast models that include cyclic behavior. The NPV can be represented as:
where = cash flow in year n and = project lifetime and i is the discount rate as a decimal. (Towler 407). If the net present value is equal to zero, the return of the project is equal to the return that the discount rate would provide. (Peters 328). There are several drawbacks to NPV; it does not measure bang for buck, and it cannot be optimized unless an upper bound is set to the plant size.
Discounted Cash Flow Rate of Return
The DCFROR is the interest or discount rate for which the NPV is equal to zero. (Turton 270). This means that DCFROR represents the highest after tax interest rate at which the project can break even. Often, corporation management will set an "internal" interest rate, which is the lowest rate of return that a company will accept for any new investment. If the DCFROR is greater than this internal rate, the investment is favorable. NPV and DCFROR are almost always used together. (Peters 328). The DCFROR can be represented as:
where i' is the DCFROR. DCFROR is useful for comparing projects of different sizes and for comparing projects to other investments. (Towler 408).
Discounted Payback Period
DPP is the time required, after start-up, to recover the fixed capital costs required for a project with all cash flows discount back to time zero. (Turton 268). The project with the shortest discounted payback period is the most desirable.
Example – Calculating NPV
Using the following projected cash flow statement, calculate the net present value using the 10 year AA corporate bond rate of 2.78%.
| Year: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Revenue | $ - | $ - | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 |
| Capital Expenditures | $ (45.00) | $ (40.00) | $ - | $ - | $ - | $ - | $ - | $ - | $ - | $ - | $ - | $ - |
| Operating Costs | $ - | $ - | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) |
| Depreciation | $ - | $ - | $ (17.00) | $ (27.20) | $ (16.32) | $ (9.79) | $ (9.79) | $ (4.90) | $ - | $ - | $ - | $ - |
| Taxes | $ - | $ - | $ (2.61) | $ 0.35 | $ (2.81) | $ (4.70) | $ (4.70) | $ (6.12) | $ (7.54) | $ (7.54) | $ (7.54) | $ (7.54) |
| Free Cash Flow | $ (45.00) | $ (40.00) | $ 23.39 | $ 26.35 | $ 23.19 | $ 21.30 | $ 21.30 | $ 19.88 | $ 18.46 | $ 18.46 | $ 18.46 | $ 18.46 |
A Net Present Value of 90.73 was obtained.
Annualized Costs
Annualized Cost is another way of comparing capital expenses with future cash flows where the capital expense is converted into a recurring annual capital charge. It is useful for comparing the cost of assets with different lifetimes. (Towler 411). This is very similar to the way that mortgages are amortized over a 15 or 30 year lifetime. Annual payment can be represented as:
where P is the principle investment, n is investment period, and i is the discount rate. The annual capital charge ratio can be defined as:
It is the fraction of the principle that must be paid each year to recover the investment at the target interest rate.
Estimating the Discount Rate
Small changes in the discount rate, can cause large fluctuations in future cash flow. When projecting project cash flows many years in the future it is essential that an accurate discount rate is chosen to get a reasonable cost estimation. A simple estimation of the discount rate is to set it equal to the interest rate received from bonds. This simple estimation will often yield a result greatly under a value needed for a good cost estimations because in the modern financial economy, cash deposits yield minimal interest rates. Many other forms of higher yielding securities are available to investors and a good discount rate should combine the interest from many different sources rather than just cash deposits.
Weighted- Average Cost of Capital. (WACC)
The weighted average cost of capital is a rate that a company is expected to pay to all of its shareholders to finance all of its assets and liabilities (debt, equity, etc.). The WACC is not a rate set by management, but is rather an implied rate that the company must return to shareholders or else they will start selling shares to invest elsewhere and depress the company’s value. Due to this reason, WACC rates for the same company can be evaluated to different estimations depending on calculation method.
Generally, WACC is described by the following formula: [3]
where is the number of sources of capital (securities, types of liabilities); is the required rate of return for security ; and is the market value of all outstanding securities .
The WACC is often simplified to include only debt and equity. Thus it can be written as
where is the total market value of shareholder’s equity, is the total market value of debt, is the cost of equity, and is the cost of debt. [4]
Cost of Equity
The cost of equity is analogous to the returns that shareholders expect in return from giving a company their equity through share purchases.
where is the risk free rate of return that investors in stable securities such as US treasury bonds can expect. is a commonly used factor describing the company’s stock’s correlation with the general market. is the risk premium, the rate of return that investors expect by investing in a stock rather than a more stable class of security. A risky company will have a higher risk premium. [5]
Cost of Debt
The cost of debt, , is either a fixed or variable rate that a company pays to a lender. This rate has been renegotiated and can be easily looked up. Since debt is tax deductible, taxes are often discounted.
WACC equation
Where is the tax rate.
Many of the inputs required to calculate WACC can be easily obtained from a publicly traded company’s financial statements. An example of some WACCs of major chemical companies as of 2/6/15 are shown in the following table. [6]
| Company | WACC |
|---|---|
| The Dow Chemical Company | 7.01% |
| Exxon Mobil Corporation | 11.64% |
| Monsanto Company | 9.23% |
Example – Comparing Interest Rate and WACC methods
Using the same projected cash flow statement as in the example of calculating NPV above, calculate the net present value using the WACC of Dow chemical company and compare it to the 10 year AA corporate bond rate.
| Year: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Revenue | $ - | $ - | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 | $ 38.00 |
| Capital Expenditures | $ (45.00) | $ (40.00) | $ - | $ - | $ - | $ - | $ - | $ - | $ - | $ - | $ - | $ - |
| Operating Costs | $ - | $ - | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) | $ (12.00) |
| Depreciation | $ - | $ - | $ (17.00) | $ (27.20) | $ (16.32) | $ (9.79) | $ (9.79) | $ (4.90) | $ - | $ - | $ - | $ - |
| Taxes | $ - | $ - | $ (2.61) | $ 0.35 | $ (2.81) | $ (4.70) | $ (4.70) | $ (6.12) | $ (7.54) | $ (7.54) | $ (7.54) | $ (7.54) |
| Free Cash Flow | $ (45.00) | $ (40.00) | $ 23.39 | $ 26.35 | $ 23.19 | $ 21.30 | $ 21.30 | $ 19.88 | $ 18.46 | $ 18.46 | $ 18.46 | $ 18.46 |
To calculate Dow Chemical’s WACC, we need the following information
- Total Equity,
- Total Debt,
- Corporate Tax Rate,
- Cost of Debt,
- Cost of Equity,
Unlike total equity, total debt and the corporate tax rate, the cost of debt and the cost of equity are not concrete numbers that are reported by most publicly traded companies. The cost of debt can be calculated by using the amount of interest that a company pays on their total debt while the cost of equity can be calculated by estimating the risk free rate, the risk premium for a market and the beta of the company. The risk free rate and the risk premium can vary slightly from model to model, but the beta is easily obtained from any financial website.
To calculate the cost of debt and the cost of equity we need the following information.
- Cost of Debt,
- Total Debt,
- Interest Payments,
- Cost of Equity,
- Risk Free Rate,
- Beta,
- Risk Premium,
Many of these variables can be easily obtained by examining Dow Chemical’s corporate filings. To find, , , , and , we can look at Dow’s annual report for 2014 found via the SEC. (http://www.sec.gov/Archives/edgar/data/29915/000002991515000011/dow201410k.htm)
| Total Equity | $ 22,423,000,000.00 |
| Total Debt | $ 18,838,000,000.00 |
| Interest Payments | $ 1,002,000,000.00 |
| Tax Rate | 27.1% |
Using these figures, the cost of debt can be calculated:
To calculate the cost of equity, the risk free rate and the risk premium need to be estimated. US treasury bonds are typically used as the benchmark for a risk free investment and the yield for a 10 year treasury bond was taken to be the risk free rate. The risk premium was taken to be the average return of the S&P 500 stock index over the previous 10 years. Finally the beta was obtained from Yahoo Finance.
| Beta | 0.75 |
| Risk Free Rate | 2.24% |
| Risk Premium | 9.37% |
Using these values, the cost of equity can be calculated:
With all necessary parameters obtained, we can estimate Dow Chemical’s WACC:
After WACC is obtained, we can compare the NPV using the WACC as the discount rate vs using the 10 year AA corporate bond rate as the discount rate.
The NPV using the 10 year AA corporate bond rate of 2.78% was found to be 90.73 in the previous example.
Calculate the NPV using a WACC of 6.81%
| WACC | 55.51 |
| 10 Year AA Corporate Bond Rate | 90.73 |
Using the 10 year AA corporate bond yield as an interest rate results in a substantial difference in net present value than using Dow Chemical’s WACC. This example highlights the need to accurately estimate the discount rate to achieve a reasonable economic evaluation.
Conclusion
Measures of economic return are vital in the design phase of an engineering project. Companies will perform simulations to project capital and operating cost expenditures along with revenue generation, and use the resulting data to perform economic analyses, such as NPV, payback period, or discounted cash flow analysis. Based on the results of this analysis, the project will either be scrapped or it will be given the go ahead to begin granular design and construction. These measures of economic return can be very sensitive to the tax rate, discount rate, and other financial factors and it is very important to provide reasonable values of these parameters to get an accurate economic return. Measures of economic return provide a quick way for companies to determine the feasibility of a project, and therefore are extremely valuable.
References
- Biegler L, Grossmann I, Westerberg A, Systematic Methods of Chemical Process Design, Prentice-Hall: Upper Saddle River, 1997.
- Douglas J, Conceptual Design of Chemical Processes, McGraw-Hill: New York, 1988.
- "EDGAR Search Results." EDGAR Search Results. U.S. Securities and Exchange Commission, n.d. Web. 06 Feb. 2015.
- Fernandes N. 2014, Finance for Executives: A Practical Guide for Managers, p. 32.
- "DCF Analysis: Calculating The Discount Rate | Investopedia." Investopedia. Investopedia, 03 Jan. 2006. Web. 06 Feb. 2015.
- Form 1120 Instructions for 2012 page 17
- Frank, Murray; Shen, Tao (2012). "Investment, Q, and the Weighted Average Cost of Capital".http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2014367.
- Miles J, Ezzell J. (September 1980). "The weighted average cost of capital, perfect capital markets and project life: a clarification". Journal of Financial and Quantitative Analysis 15 (3): 719–730.doi:10.2307/2330405.
- Peters M, Timmerhaus K, "Plant Design and Economics for Chemical Engineers", 5th Ed., McGraw-Hill: New York, 2003
- Sieder W, Seader J, Lewin D, Process Design Principles: Synthesis, Analysis, and Evaluation, Wiley: New York, 2004.
- Towler G, Sinnott R, Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design, Elsevier, 2012.
- Turton R, Bailie R, Whiting W, Shaeiwitz J, Analysis, Synthesis, and Design of Chemical Processes, Prentice Hall: Upper Saddle River, 2003.