Pressure changer: Difference between revisions
Kedricdaly2 (talk | contribs) |
Kedricdaly2 (talk | contribs) m →Pumps: spacing |
||
| Line 21: | Line 21: | ||
</center> | </center> | ||
Where <math> \mathbf{P} </math> is the power required, <math> m </math> is the mass flow rate, <math> W_s </math> is that shaft work, <math> u </math> is the velocity of the fluid, <math> \alpha </math> describes the flow in the system (0.5 for laminar, 1 for turbulent), <math> g </math> is the gravitational acceleration, <math> \Delta z </math> is the change in height, <math> \int_{P_1}^{P_2} vdP </math> is the constant volume PV work done, and <math> F </math> is the force acting on the fluid. Each grouping deals with different aspects of the fluid flow. The first term deals with the kinetics, the second term with the statics, the third term with the pressure head, and the fourth term with the viscous losses. <ref name="Pressure Changers"> YA Hussein. Pressure Changers. Available at http://www.just.edu.jo/~yahussain/files/Pressure%20Changers.pdf Accessed February 3, 2016</ref> It should also be noted that a pressure head is the height of a fluid that results in an equivalent pressure via the <math> P = \rho g h </math> relation. | Where <math> \mathbf{P} </math> is the power required, <math> m </math> is the mass flow rate, <math> W_s </math> is that shaft work, <math> u </math> is the velocity of the fluid, <math> \alpha </math> describes the flow in the system (0.5 for laminar, 1 for turbulent), <math> g </math> is the gravitational acceleration, <math> \Delta z </math> is the change in height, <math> \int_{P_1}^{P_2} vdP </math> is the constant volume PV work done, and <math> F </math> is the force acting on the fluid. Each grouping deals with different aspects of the fluid flow. The first term deals with the kinetics, the second term with the statics, the third term with the pressure head, and the fourth term with the viscous losses. <ref name="Pressure Changers"> YA Hussein. Pressure Changers. Available at http://www.just.edu.jo/~yahussain/files/Pressure%20Changers.pdf Accessed February 3, 2016</ref> It should also be noted that a pressure head is the height of a fluid that results in an equivalent pressure via the <math> P = \rho g h </math> relation. | ||
<br/> | |||
<br/><br/> | |||
While the mechanical balance equation can be used to find the outlet power required, no pump is 100% efficient. The efficiency, <math> \eta </math>, of a pump is defined as: | While the mechanical balance equation can be used to find the outlet power required, no pump is 100% efficient. The efficiency, <math> \eta </math>, of a pump is defined as: | ||
Revision as of 22:44, 4 February 2016
Authors: Kedric Daly [2016]
Stewards: David Garcia, Fengqi You
Date Presented: February 5, 2016
Introduction
Pressure changers are any piece of equipment where the main goal is to increase or decrease the pressure of a stream. Typically, pressure changers are used mostly for increasing pressure, due to the fact that pressure losses occur within a system due to friction with pipes, pipe bends, valves, and other pieces of equipment [1]. Lowering the pressure of a system can also be useful however, such as to favor the products of a chemical reaction through Le Chatelier's principle. It is important however to ensure proper pressure is maintained throughout a chemical process so that blowback does not occur, and any fluids actually reach their destination as expected, at the proper conditions.
There are many different types of modeling software for chemical processing, Aspen HYSYS, and Aspen Plus being well known. Like any piece of process equipment, it is necessary to specify a number of independent variables in order for the simulation to converge and produce unknown values. There are different combinations of independent variables that will suffice and cause the model to converge. Different parameters of the pump or compressor can also be specified, such as efficiency, which will impact the results of the simulation. It is therefore important to ensure the equipment is correctly specified to ensure accurate results.
Pumps
Pumps do work on fluids, causing them to increase in pressure at a constant volume, due to the assumption that liquids that enter pumps are mostly incompressible. To find the power outlet required by a pump to pressurize a fluid, an energy balance can be done on the system. The result is the mechanical balance equation, below:
Where is the power required, is the mass flow rate, is that shaft work, is the velocity of the fluid, describes the flow in the system (0.5 for laminar, 1 for turbulent), is the gravitational acceleration, is the change in height, is the constant volume PV work done, and is the force acting on the fluid. Each grouping deals with different aspects of the fluid flow. The first term deals with the kinetics, the second term with the statics, the third term with the pressure head, and the fourth term with the viscous losses. [2] It should also be noted that a pressure head is the height of a fluid that results in an equivalent pressure via the relation.
While the mechanical balance equation can be used to find the outlet power required, no pump is 100% efficient. The efficiency, , of a pump is defined as:
The efficiency of a pump is related to the pressure head and the fluid flow rate because the work can be converted to either a higher velocity or a larger pressure head.[2]. Manufacturers often supply characteristic pump curves in order to inform their customers which pumps will meet their needs. An example curve can be seen below.
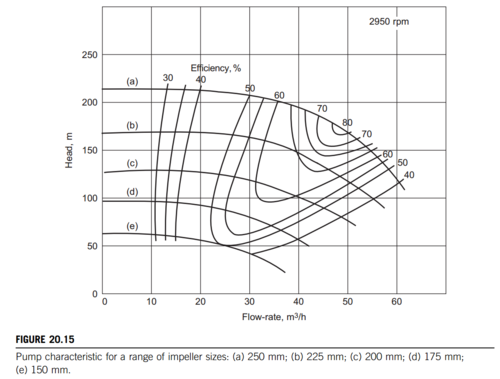
References
- ^ a b G.P. Towler, R. Sinnott, Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design, Elsevier, 2012
- ^ a b YA Hussein. Pressure Changers. Available at http://www.just.edu.jo/~yahussain/files/Pressure%20Changers.pdf Accessed February 3, 2016